Тригонометрия
Большая Советская Энциклопедия. Статьи для написания рефератов, курсовых работ, научные статьи, биографии, очерки, аннотации, описания.
|
|
| ТРА |
| ТРД |
| ТРЕ |
| ТРЁ |
| ТРИ |
| ТРН |
| ТРО |
| ТРП |
| ТРУ |
| ТРШ |
| ТРЮ |
| ТРЯ |
Тригонометрия (от греч. trígōnon — треугольники ¼метрия), раздел математики, в котором изучаются тригонометрические функции и их приложения к геометрии. Тригонометрия делится на плоскую, или прямолинейную, и сферическую тригонометрию. Теория тригонометрических функций (гониометрия) и её приложения к решению плоских прямоугольных и косоугольных треугольников изучаются в средней школе.
Основные формулы плоской Тригонометрия Пусть а, b, с — стороны треугольника, А, В, С — противолежащие им углы (А+В+С = p), ha, hb, hc — высоты, 2p — периметр, S — площадь, 2R — диаметр окружности, описанной около треугольника. Теорема синусов:
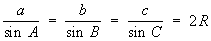 ,
,
теорема косинусов:
a2 = b2 + c2 — 2bc cos A,
теорема тангенсов:
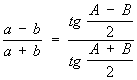 ,
,
площадь треугольника:
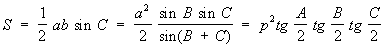 .
.
Углы треугольника, если известны стороны, могут быть найдены по теореме косинусов или по формулам вида:
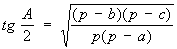 .
.
Плоская Тригонометрия начала развиваться позже сферической, хотя отдельные теоремы её встречались и раньше. Например, 12-я и 13-я теоремы второй книги «Начал» Евклида (3 в. дон. э.) выражают по существу теорему косинусов. Плоская Тригонометрия получила развитие у аль-Баттани (2-я половина 9 — начало 10 вв.), Абу-ль-Вефа (10 в.), Бхаскара (12 в.) и Насирэддина Туси (13 в.), которым была уже известна теорема синусов. Теорема тангенсов была получена Региомонтаном (15 в.). Дальнейшие работы в области Тригонометрия принадлежат Н. Копернику (1-я половина 16 в.), Тригонометрия Браге (2-я половина 16 в.), Ф. Виету (16 в.), И. Кеплеру (конец 16 — 1-я половина 17 вв.). Современный вид Тригонометрия получила в работах Л. Эйлера (18 в.).
Лит.: Кочетков Е. С., Кочеткова Е. С., Алгебра и элементарные функции, ч. 1—2, М., 1966.
|
Так же Вы можете узнать о... Штраус Рихард Штраус (Strauß) Рихард (11. Вальдепеньяс (Valdepeňas), город в Центральной Испании, в Новой Кастилии (провинция Сьюдад-Реаль), на р. Заславская Суламифь Александровна (р. 7.3.1918, Черкассы), советский мастер художественного текстиля. Линна Вяйнё Валттери Линна (Linna) Вяйнё Валттери (р. 20.12.1920, деревня Урьяла), финский писатель. Пеория (Peoria), город в США, в штате Иллинойс, на р. Спендиаров Александр Афанасьевич Спендиаров (настоящая фамилия — Спендиарян) Александр Афанасьевич [20. Чойбалсан Хорлогийн (8.2.1895, Цэцэнханский, ныне Восточный, аймак, — 26. Бош Евгения Богдановна (Готлибовна) [11(23). Дятлы, семейство птиц отряда дятлообразных; то же, что дятловые. Лаланд Андре Лаланд (Lalande) Андре (19.7.1867, Дижон, — 15. Отрицания отрицания закон, один из основных законов диалектики, характеризующий направление процесса развития, единство поступательности и преемственности в развитии, возникновения нового и относительной повторяемости некоторых моментов старого. Славяно-греко-латинская академия, первое высшее общеобразовательное учебное заведение в Москве. Центральный Дом литераторов (ЦДЛ), см. Дом литераторов. Бессмертнова Наталья Игоревна (р. 19.7.1941, Москва), советская артистка балета, народная артистка СССР (1976). Динамическая геология, физическая геология, направление геологии, изучающее геологические процессы, протекающие в земной коре и на её поверхности. Кричнорудный процесс, круппренн-процесс, современная модификация сыродутного процесса, представляющая собой непосредственное (минуя доменную печь) получение железа из руд; предназначается для переработки бедных труднообогатимых или комплексных железных руд во вращающихся трубчатых печах с целью получения крицы. |
|