Последовательный анализ
Большая Советская Энциклопедия. Статьи для написания рефератов, курсовых работ, научные статьи, биографии, очерки, аннотации, описания.
|
|
| ПОА |
| ПОБ |
| ПОВ |
| ПОГ |
| ПОД |
| ПОЕ |
| ПОЖ |
| ПОЗ |
| ПОИ |
| ПОЙ |
| ПОК |
| ПОЛ |
| ПОМ |
| ПОН |
| ПОО |
| ПОП |
| ПОР |
| ПОС |
| ПОТ |
| ПОУ |
| ПОХ |
| ПОЦ |
| ПОЧ |
| ПОШ |
| ПОЭ |
| ПОЯ |
Последовательный анализ в математической статистике, способ статистической проверки гипотез, при котором необходимое число наблюдений не фиксируется заранее, а определяется в процессе самой проверки. Во многих случаях для получения столь же обоснованных выводов применение надлежащим образом подобранного способа Последовательный анализ позволяет ограничиться значительно меньшим числом наблюдений (в среднем, т.к. число наблюдений при Последовательный анализ есть величина случайная), чем при способах, в которых число наблюдений фиксировано заранее.
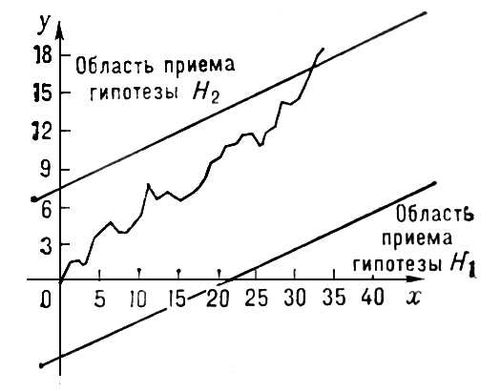
Графическое изображение процесса последовательного анализа.
Пусть, например, задача состоит в выборе между гипотезами H1 и H2 по результатам независимых наблюдений. Гипотеза H1 заключается в том, что случайная величина Х имеет распределение вероятностей с плотностью f1(x), a H2 — в том, что Х имеет плотность f2(x). Для решения этой задачи поступают следующим образом. Выбирают два числа А и В (0 < A < B). После первого наблюдения вычисляют отношение l1 = f2(x1)/f1(x1), где x1— результат первого наблюдения. Если l1 < A, принимают гипотезу H1; если l1 > B, принимают H2, если A£l1 £B, производят второе наблюдение и так же исследуют величину l2 = f2(x1) f2(x2)/f1(x1) f1(x2), где x2 — результат второго наблюдения, и т.д. С вероятностью, равной единице, процесс оканчивается либо выбором H1, либо выбором H2. Величины А и В определяются из условия, чтобы вероятности ошибок первого и второго рода (т. е. вероятность отвергнуть гипотезу H1, когда она верна, и вероятность принять H1, когда верна H2) имели заданные значения a1 и a2. Для практических целей вместо величины ln удобнее рассматривать их логарифмы. Пусть, например, гипотеза H1 состоит в том, что Х имеет нормальное распределение 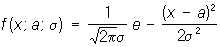
с a = 0,s = 1, гипотеза H2 — в том, что X имеет нормальное распределение с a = 0,6, s = 1, и пусть a1 = 0,01, a2 = 0,03. Соответствующие подсчёты показывают, что в этом случае 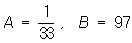 и logln = 0.6
и logln = 0.6 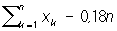
Поэтому неравенства 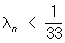 и
и 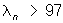 равносильны неравенствам
равносильны неравенствам 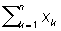 < 0.3n 5.83
< 0.3n 5.83 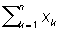 > 0.3n + 7.62
> 0.3n + 7.62
соответственно. Процесс Последовательный анализ допускает при этом простое графическое изображение (см. рис.). На плоскости (хОу) наносятся две прямые y = 0.3x 5.83 и y = 0.3x + 7.62 и ломаная линия с вершинами в точках (n, 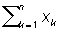 ), n = 1, 2,.... Если ломаная впервые выходит из полосы, ограниченной этими прямыми, через верхнюю границу, то принимается H2, если через нижнюю, — H1. В приведённом примере для различения H1 и H2методом Последовательный анализ требуется в среднем не более 25 наблюдений. В то же время для указанного различения гипотез H1 и H2 по выборкам фиксированного объёма потребовалось бы более 49 наблюдений.
), n = 1, 2,.... Если ломаная впервые выходит из полосы, ограниченной этими прямыми, через верхнюю границу, то принимается H2, если через нижнюю, — H1. В приведённом примере для различения H1 и H2методом Последовательный анализ требуется в среднем не более 25 наблюдений. В то же время для указанного различения гипотез H1 и H2 по выборкам фиксированного объёма потребовалось бы более 49 наблюдений.
Лит.: Блекуэлл Д., Гиршик М. А., Теория игр и статистических решений, пер. с англ., М., 1958: Вальд А., Последовательный анализ, пер. с англ., М., 1960; Ширяев А. Н., Статистический последовательный анализ, М., 1969.
|
Так же Вы можете узнать о... Шмели (Bombidae), семейство крупных пчёл. Тело длиной до 3,5 см, густо покрыто волосками, окраска из сочетания чёрных, белых, ярко-рыжих и жёлтых полос. Эль-Халиль, Хеброн, Хеврон, город в западной части Иордании, в 30 км к Ю. Яровая, посёлок городского типа в Краснолиманском районе Донецкой области УССР. Ала-ад-дин Хильджи, правитель [1296 — 1316] Делийского султаната. Антре [франц. entreе — вход, вступление, выход (на сцену)], Ашофф Карл Альберт Людвиг Ашофф (Aschoff) Карл Альберт Людвиг (10.1.1866, Берлин, — 24. Белл Александер Грейам Белл (Bell) Александер Грейам (3.3.1847, Эдинбург, Шотландия, — 2. Болгарской Народной Республики-Германской Демократической Республики договор 1967 Болгарской Народной Республики — Германской Демократической Республики договор 1967 О дружбе, сотрудничестве и взаимной помощи, подписан в Софии 7 сентября со стороны НРБ первым секретарём ЦК БКП, председателем Совета Министров НРБ Т. Бывальщина (также быль), в русском народном творчестве короткий устный рассказ о каком-либо случае, будто бы имевшем место в действительности, о невероятных происшествиях, о найденных кладах, о встречах с "нечистой силой". Ветеринарно-санитарная экспертиза, 1) научная дисциплина, разрабатывающая методы исследования и ветеринарно-санитарной оценки продуктов животного происхождения. Ворохта, посёлок городского типа в Надворнянском районе Ивано-Франковской области УССР, на р. Гвадаррама (Guadarrama), горная цепь в Испании; см. «Глобус» (Globe Theatre), театр в Лондоне. Построен в 1599. Грушевая эссенция, спиртовой раствор смеси сложных эфиров алифатических карбоновых кислот с преобладающим содержанием амилацетата. Дессау (город в ГДР) Дессау (Dessau), город в ГДР, на р. Мульда, близ её впадения в Эльбу, в округе Галле. |
|