Плотность вероятности
Большая Советская Энциклопедия. Статьи для написания рефератов, курсовых работ, научные статьи, биографии, очерки, аннотации, описания.
|
|
| ПЛА |
| ПЛЕ |
| ПЛЁ |
| ПЛИ |
| ПЛО |
| ПЛУ |
| ПЛЫ |
| ПЛЬ |
| ПЛЮ |
| ПЛЯ |
Плотность вероятности случайной величины X, функция р(х), такая, что при любых a и b вероятность неравенства а < Х < b равна 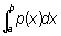 .
.
Например, если Х имеет нормальное распределение, то 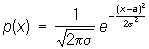 .
.
Если Плотность вероятности p(x) непрерывна, то при достаточно малых dx вероятность неравенства x < X < x + dx приближённо равна p(x)dx. Плотность вероятности всегда удовлетворяет условиям 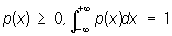 .
.
Аналогично определяют Плотность вероятности p(x1,...,xs) для нескольких случайных величин X1, X2, ...,Xs(т. н. совместную Плотность вероятности): при любых ai, biвероятность одновременного выполнения неравенств a1 < Xi < b1, . . ., as < Xs < bsравна 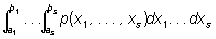 .
.
Если существует совместная Плотность вероятности X1, Х2, ..., Xs, то для независимости этих величин необходимо и достаточно. чтобы совместная Плотность вероятности была произведением Плотность вероятности отдельных величин Xi,i = 1, 2, . . ., s.
|
Так же Вы можете узнать о... Постановщик, режиссёр-постановщик, творческий работник, осуществляющий постановку спектакля, фильма. Скарлатти Доменико Скарлатти (Scarlatti) Доменико (26.10.1685, Неаполь, — 23. Уичито-Фолс (Wichita Falls), город на Ю. США, в штате Техас, на р. Шувелян, посёлок городского типа в Азербайджанской ССР, подчинён Азизбековскому райсовету г. Баласогло Александр Пантелеймонович [23.10(4. Вышелесский Сергей Николаевич (20.10.1874, Оболь, ныне Витебской области БССР, — 14. Ежи (семейство млекопитающих) Ежи (Erinaceidae), семейство млекопитающих отряда насекомоядных (Insectivora). Ковалевская Софья Васильевна [3(15).1.1850, Москва, — 29. Малышев Илья Ильич [19.7(1.8). 1904, посёлок Майкор, ныне Коми-Пермяцкого национального округа Пермской области, — 23. Октябрьский (пос. гор. типа в Горьковской обл.) Октябрьский, посёлок городского типа в Борском районе Горьковской области. Радиочувствительность, чувствительность биологических объектов к действию ионизирующих излучений. «Старина и новизна», русский исторический сборник, издававшийся «Обществом ревнителей рус. Форкамера, полость в головке цилиндра двигателя внутреннего сгорания; то же. Юрумкувеем (в низовье — Белая), река в Магаданской области РСФСР, левый приток Анадыря. Блондель Шарль Блондель (Blondel) Шарль (10.10.1876, Лион, — 19. Гиршман Роман Гиршман (Ghirshman) Роман (р. 3.10.1895, Харьков), французский археолог и историк Ближнего и Среднего Востока. Ибн Сина Абу Али Хусейн ибн Абдаллах Ибн Сина, Абу Али Хусейн ибн Абдаллах (латинизированное — Авиценна) (980, с. |
|