Золотое сечение
Большая Советская Энциклопедия. Статьи для написания рефератов, курсовых работ, научные статьи, биографии, очерки, аннотации, описания.
|
|
| ЗОБ |
| ЗОГ |
| ЗОД |
| ЗОЕ |
| ЗОЗ |
| ЗОИ |
| ЗОЙ |
| ЗОЛ |
| ЗОМ |
| ЗОН |
| ЗОО |
| ЗОП |
| ЗОР |
| ЗОС |
| ЗОТ |
| ЗОУ |
| ЗОФ |
| ЗОХ |
| ЗОЩ |
Золотое сечение, гармоническое деление, деление в крайнем и среднем отношении, деление отрезка AB на две части т. о., что большая его часть AC является средней пропорциональной между всем отрезком AB и меньшей его частью CB (см. рис.). Алгебраическое нахождение Золотое сечение отрезка AB = а сводится к решению уравнения a/x = х/(а—х) (где х = AC), откуда 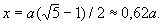
Рис. к ст. Золотое сечение.
Отношение х к а может быть также выражено приближённо дробями 2/3, 3/5, 5/8, 8/13, 13/21 и т.д., где 2, 3, 5, 8, 13, 21 и т.д. — Фибоначчи числа. Геометрически построение Золотое сечение отрезка AB осуществляется так: в точке В проводят перпендикуляр к AB, откладывают на нём отрезок BE = 1/2AB, соединяют А и Е, откладывают ED = EB и, наконец, AC = AD, тогда будет AB/AC = AC/CB. Золотое сечение было известно ещё в древности. В дошедшей до нас античной литературе Золотое сечение впервые встречается в «Началах» Евклида (3 в. до н. э.). Термин «Золотое сечение» ввёл Леонардо да Винчи (конец 15 — начало 16 вв.). Принципы Золотое сечение или близкие ему пропорциональные отношения легли в основу композиционного построения многих произведений мирового искусства (главным образом произведений архитектуры античности и Возрождения).
|
Так же Вы можете узнать о... Торез (город в Донецкой обл.) Торез (до 1964 — Чистяково), город областного подчинения в Донецкой области УССР. Тулуз-Лотрек Анри Мари Раймон де Тулуз-Лотрек (Toulouse-Lautrec) (собственно Тулуз-Лотрек-Монфа, Toulouse-Lautrec-Monfa) Анри Мари Раймон де (24. Ультиматисты, левооппортунистическая группа, образовавшаяся в РСДРП в 1908 (Г. Фанатизм (франц. fanatisme, от лат. fanaticus – исступлённый), доведённая до крайней степени приверженность к каким-либо верованиям или воззрениям, нетерпимость к любым другим взглядам, например религиозный Ф. Фламинго (Phoenicopteri), отряд птиц. Часто включается как подотряд в отряд голенастых. Фукуока (префектура в Японии) Фукуока, префектура в Японии, в северной части о. «Хиндустан таймс», «Хиндустан таймс груп» (Hindustan Times Group), индийская газетная корпорация. Цейс Карл Фридрих Цейс (Zeiss) Карл Фридрих (11.9.1816, Веймар, — 3. Чебышева многочлены , Шабазит, минерал группы цеолитов; химический состав (Ca, Na2, K2) Al2Si3¾8O10¾20. Шлюзование судов, см. в ст. Шлюз судоходный. Экваториальные течения, см. Пассатные течения. Энценсбергер Ханс Магнус Энценсбергер (Enzensberger) Ханс Магнус (р. 11. Яворский Болеслав Леопольдович [10(22).6.1877, Харьков, — 26. |
|
