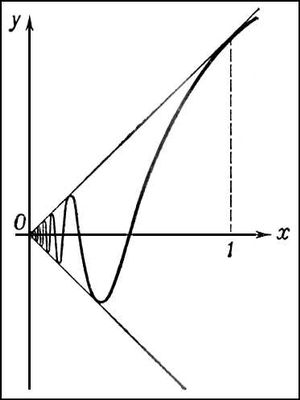
Длина, числовая характеристика протяжённости линий. В разных случаях понятие Длина определяется различно. 1) Длина отрезка прямой — расстояние между его концами, измеренное каким-либо отрезком, принятым за единицу Длина 2) Длина ломаной — сумма Длина её звеньев. 3) Длина простой дуги — предел Длина вписанных в эту дугу ломаных, когда число звеньев неограниченно увеличивается и максимальная Длина звеньев стремится к нулю. 4) Длина непрерывной кривой, состоящей из конечного числа простых дуг, равна сумме Длина этих дуг. Например, Длина окружности может быть получена как предел периметров правильных вписанных многоугольников при неограниченном удвоении числа их сторон и равна 2pR, где R — радиус окружности. Всякая непрерывная кривая имеет Длина — конечную или бесконечную. Если её Длина конечна, то кривая называется спрямляемой. График функции (см. рис.)  

Рис. к ст. Длина.

даёт пример неспрямляемой кривой; здесь Длина вписанных ломаных неограниченно растут, когда Длина звеньев стремятся к нулю. Если уравнение плоской кривой в прямоугольных координатах имеет вид у = f (x) (a£x£b), причём функция f (x) имеет непрерывную производную f¢ (x), то Длина кривой выражается интегралом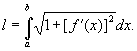  

Аналогично выражается Длина кривой, заданной параметрически, и Длина пространственной кривой.

  К вычислению Длина кривой при помощи предельного перехода из Длина ломаных прибегали по существу ещё математики древности. Для них, однако, этот предельный переход был лишь способом вычисления Длина кривой, а не определения понятия Длина кривой, т.к. последнее им представлялось, по-видимому, одним из первоначальных математических понятий. Необходимость определения Длина кривой стала ясной лишь в 1-й половине 19 в. Полное выяснение вопроса было достигнуто К. Жорданом. В дифференциальной геометрии определяется также Длина кривой на поверхности или в произвольном римановом пространстве. О единицах и технике измерения Длина см. Меры длины, Измерение.

 

  Лит.: Лебег А., Об измерении величин, пер. с франц., 2 изд., М., 1960; Фихтенгольц Г. М., Курс дифференциального и интегрального исчисления, 7 изд., т. 2, М., 1969.

  С. Б. Стечкин.