Графов теория
Большая Советская Энциклопедия. Статьи для написания рефератов, курсовых работ, научные статьи, биографии, очерки, аннотации, описания.
|
|
| ГРА |
| ГРЕ |
| ГРЁ |
| ГРЖ |
| ГРИ |
| ГРО |
| ГРУ |
| ГРЫ |
| ГРЭ |
| ГРЮ |
| ГРЯ |
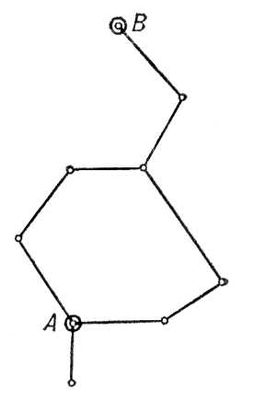
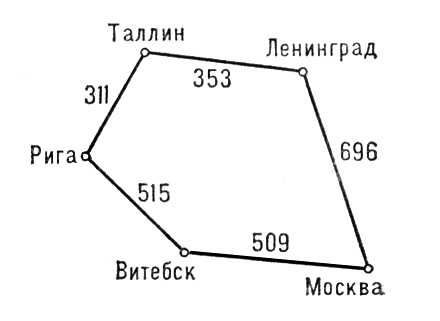
Графов теория, раздел конечной математики, особенностью которого является геометрический подход к изучению объектов. Основное понятие теории — граф. Граф задаётся множеством вершин (точек) и множеством рёбер (связей), соединяющих некоторые (а может быть, и все) пары вершин. При этом пары вершин могут соединяться несколькими ребрами. Примеры графов: множество городов (вершины графа), например Московской области, и соединяющие их дороги (ребра графа); элементы электрической схемы и провода, соединяющие их. На рис. 1 изображен граф, вершинами которого являются станции городского метрополитена, а ребрами — пути, соединяющие соседние станции (одна из задач: указать какой-либо маршрут от станции А к станции В). Граф называется ориентированным, если на ребрах задана ориентация, т. е. указан порядок прохождения вершин. Наконец, в Графов теория изучаются графы, у которых ребрам приписаны какие-либо веса (или символы), а также графы, в которых выделены особые вершины, называются полюсами. Примеры: диаграмма состояний автомата, сеть ж.-д. путей с указанием на дугах их длин или пропускных способностей. На рис. 2 приведена схема автомобильных дорог между Москвой и Таллином; надо, например, выбрать маршрут минимальной общей длины пути из Москвы в Таллин (эти два города — полюсы сети); сравнение двух маршрутов Москва — Ленинград — Таллин и Москва — Витебск — Рига — Таллин показывает, что путь через Ленинград короче (1049 км).
Рис. 1 к ст. Графов теория.
Рис. 2 к ст. Графов теория.
Одной из первых работ по Графов теория можно считать работу Л. Эйлера (1736), относящуюся к решению головоломок и математических развлекательных задач. Первые глубокие результаты были получены в 1-й половине 20 в. в связи с решением задач построения электрических цепей и подсчёта химических веществ с различными типами молекулярных соединений. Однако широкое развитие Графов теория получила лишь с 50-х гг. в связи со становлением кибернетики и развитием вычислительной техники, когда Графов теория существенно обогатилась и новым материалом, и новыми подходами и когда началось систематическое изучение графов с разных точек зрения (структурной, информационной и т. д.). Именно в это время формулировались проблематика и методы Графов теория Графов теория находит применение в теории программирования и при построении вычислительных машин, в изучении физических, химических и технологических процессов, в решении задач планирования, в лингвистических и социологических исследованиях и т. д. Графов теория имеет тесные связи как с классическими, так и с новыми разделами математики; это — топология, алгебра, комбинаторный анализ, теория чисел, теория минимизации булевских функций. Графов теория включает большое число разнообразных задач. Одни из них группируются в отдельные направления, другие стоят более изолированно. Среди сложившихся разделов Графов теория следует отметить задачи, относящиеся к анализу графов, определению различных характеристик их строения, например выяснение связности графа: можно ли из любой вершины попасть в любую; подсчёт графов или их частей, обладающих заданными свойствами, например подсчёт количества деревьев с заданным числом рёбер (дерево — неориентированный граф без циклов); решение транспортных задач, связанных с перевозками грузов по сети. Решен ряд задач по синтезу графов с заданными свойствами, например построение графа с заданными степенями вершин (степень вершины — число выходящих из неё рёбер). Имеет прикладное и теоретическое значение задача о выяснении возможности расположения графа на плоскости без самопересечений его рёбер (т. е. является ли данный граф плоским), задача о разбиении графа на минимальное число плоских графов. Для некоторых задач Графов теория (выше были приведены далеко не все) были разработаны методы их решения. Среди них: метод Пойя перечисления и подсчёта графов с заданными свойствами, теорема и алгоритм Форда — Фалкерсона для решения транспортной задачи, «венгерский» алгоритм решения задачи о назначениях и т. д. Почти все задачи теории конечных графов (практически интересны именно графы с конечным числом вершин) могут быть решены путём перебора большого числа вариантов (т. н. полный перебор), поэтому для них требуется построение эффективных алгоритмов и использование быстродействующих вычислительных машин. Такими задачами являются: задача о раскраске вершин графа, задача об определении идентичности двух графов, коммивояжёра задача. Есть задачи, требующие принципиального ответа, например задача о раскраске плоских графов, задача о восстановлении графа по его подграфам.
Лит.: Берж К., Теория графов и её применения, пер. с франц., М., 1962; Оре О., Графы и их применение, пер. с англ., М., 1965; Зыков А. А., Теория конечных графов. I, Новосибирск, 1969.
|
Так же Вы можете узнать о... Мерефа, город (с 1938) в Харьковском районе Харьковской области УССР, на р. Электрические органы, парные образования у ряда рыб, способные генерировать электрические разряды; служат для защиты, нападения, внутривидовой сигнализации и ориентации в пространстве. Лешно (Leszno), город в Польше, в Познанском воеводстве. Цветная аэрофотосъёмка, фотографирование местности с воздуха в целях воспроизведения в натуральных цветах её ландшафтов или отдельных объектов. Кооперация жилищная, вид кооперации, члены которой объединяются для совместно строительства и эксплуатации жилых домов. Физики теоретической институт им. Л. Д. Ландау АН СССР (ИТФ), научно-исследовательское учреждение, в котором ведутся исследования по основным направлениям теоретической физики (разработка фундаментальных вопросов физики твёрдого тела и физики низких температур, теория элементарных частиц, плазмы, лазерного излучения и т. Кистяковский Владимир Александрович [30.9(12. Тюмюр, тумыр, старинный марийский ударный музыкальный инструмент. Капиллярное кровообращение движение крови в мельчайших сосудах — капиллярах обеспечивающее обмен веществ между кровью и тканями, К. Тёрка, радула (от лат. radula — скребок, скребница), аппарат, служащий для соскрёбывания и размельчения пищи у моллюсков (кроме двустворчатых). Инозит, гексаоксициклогексан, циклит, циклический шестиатомный спирт. Сума, река на В. Карельской АССР. Длина 164 км, площадь бассейна 2020 км2. Запрудня, посёлок городского типа в Талдомском районе Московской области РСФСР. «Соседи», основная категория феодально-зависимых крестьян в средневековой Молдавии; см. Доскональность (от польск. doskonałość), точность, тщательность, основательность, безупречность. |
|